NBA 선수 Stat 데이터분석 pt3- Classification과 PCA

Category: Technology

<NBA 선수 Stat 데이터 분석 - Classification>


분석에 들어가기 전에

지난번에 이어서, 이번에는 Classification을 진행해보도록 하자. 지난번까지는 어시스트, 득점, 파울 세 가지의 특성(feature)만을 사용했었다. 그러나, 역서 모든 수치 특성 (numerical feature)를 다 사용한다면 더 정확한 모델을 만들 수 있지 않을까 하는 생각이 들었다. 그래서 이번에는 이름과 같은 텍스트 형태의 데이터와, 년도, 나이, 번호와 같이 직접적인 포지션 분류와 영향이 없다고 판단되는 특성을 제외한 나머지 모든 특성을 사용해보기로 했다. 

original_data = df._get_numeric_data()
del original_data["Unnamed: 0"]
del original_data["Year"]
del original_data["Age"]

original_label = df[["New_Pos"]]

true_label = np.array(original_label)[:, 0]

positions = list(set([i[0] for i in df[["New_Pos"]].values]))
positions = sorted(positions) #order 섞이는것 방지

아예 특성들을 정리하는김에 데이터와 레이블 부분을 따로 나누어 놓았다. Classification에서는 레이블과 데이터 부분을 나누어 학습 모델을 훈련시키고, 실제 레이블과 예측된 레이블을 비교하는 작업을 거칠 것이기 때문이다. 

이렇게 하니 선수 한명당 총 45개의 특성 (Attribute)이 나왔다. 목록은 다음과 같다:

['G', 'GS', 'MP', 'PER', 'TS%', '3PAr', 'FTr', 'ORB%', 'DRB%', 'TRB%', 'AST%', 'STL%', 'BLK%', 'TOV%', 'USG%', 'OWS', 'DWS', 'WS', 'WS/48', 'OBPM', 'DBPM', 'BPM', 'VORP', 'FG', 'FGA', 'FG%', '3P', '3PA', '3P%', '2P', '2PA', '2P%', 'eFG%', 'FT', 'FTA', 'FT%', 'ORB', 'DRB', 'TRB', 'AST', 'STL', 'BLK', 'TOV', 'PF', 'PTS']

NBA Stat을 보는법은 NBA홈페이지나, 구글링을 통해 자세히 알아보길 바란다. 간단히 설명하자면 스틸, 블락, 자유투, 리바운드, 3점슛, 경기 시간 등 경기에서 행하는 행동과 관련된 모든 기록이 담겨있다.  그럼 이제 이 데이터가 어떻게 생겼는지 간단히 그래프를 통해 알아보자. 

이 데이터는 변수가 무려 45개나 되고, 데이터 포인트가 10,000개가 훌쩍 넘는 데이터이다. 이 데이터를 어떻게 좌표평면에 그려야 할까? 45차원 그래프라도 그려야 하는것일까? 그렇지만 우리가 그릴 수 있는 그래프는 3차원까지이다. 그렇다면 어떻게 이 데이터를 좌표면에 그려넣을 수 있을까?

PCA (Principa Component Analysis) - 주성분분석

나는 PCA (Principal Component Analysis) - 주성분분석 - 을 사용해보기로 했다. 예전에 전공수업에서  많은 특성 (feature)를 가진 데이터에 대해 classification을 진행하면서 PCA 를 사용했던 적이 있었지만, 그때는 그저 그래프를 그리기 위해 정확히 PCA가 뭔지 이해하지 못하고 사용했었다. 이번 기회에 PCA에 대해 더 깊히 알아보게 되었다.

기본적으로 PCA는 차원을 축소하는 방법 중의 하나이다. 데이터에서의 '차원'은 feature의 갯수를 말한다. 즉, 지난번의 게시물에서 '득점', '어시스트', '파울' 세 개의 feature를 변수로 가지고 있었을 때는 3차원의 데이터를 사용한 것이다. 즉, 원래는 48차원이나 되는 데이터에서 3개의 차원을 '추출'하여 3차원의 데이터로 만든 것이다. 데이터의 차원이 너무 많아지면 몇 가지 문제가 생긴다. 일단 첫번째로, KNN (K Nearest Neighbor)알고리즘을 포함한 많은 알고리즘이 데이터 포인트간의 거리를 기준으로 구성된다. 특히 우리가 일반적으로 쓰는 'Euclidian Distance' (유클리드 거리)를 사용한다.

예컨데, K nearest neighber 알고리즘은 데이터 포인트로부터 가장 가까운 K 개의 '이웃 데이터' 의 class(label)이 뭔지를 기준으로 데이터 포인트의 class를 결정한다. 위의 그림은 2차원 평면에 그려졌고, x축과 y축기 각각 데이터의 특성 하나씩을 나타내는 2차원의 데이터일 것이다. 만일 변수가 3개인 데이터라면 3차원 평면에 그려질 것이고, 데이터 포인트 A와 일정한 거리만큼 떨어져있는 점을 이으면 원이 아닌 '구'가 될 것이다. 그럼 4차원 이상이라면, 40차원, 50차원 이렇게 고차원이 된다면 거리를 어떻게 계산해야하는가? 점 A 로부터 일정 거리가 떨어진 점들을 모두 이었을 때 50차원 도형이 나오게 될 것이다. 우리가 일반적으로 생각하는 유클리드 거리의 계산이 통하지 않게된다. 두 번째로 차원이 너무 많으면 오히려 정확하지 않은 분석 결과가 나올수도 있다. 데이터의 차원이 많아지면 낮은 차원에서는 알 수 없던 정보를 알 수 있다. 예를들어서, 키와 몸무게를 통해서는 알 수 없던 건강정보를 수면시간, 식습관, 운동량 등의 변수를 추가해서 알아낼 수 있듯 말이다. 그러나 너무 많은 정보가 한번에 개입되어 버리면 오히려 유의미한 결과를 얻지 못할 수 있다. (다음 기사 를 참고해보자.) 이런것을 바로 '차원의 저주'라고 부른다.  이럴 경우, 차원을 선별하여 뽑는 방법이 있을 수 있지만 (지난번에 세 가지 feature를 뽑아 사용한 것처럼) 그렇게되면 많은 특성들을 반영하지 못하는 문제가 생긴다. 그래서, 모든 특성을 반영하면서 차원을 축소시키는 PCA방법을 사용한다. 

차원을 축소시키는 기본적인 원리는, 고차원의 데이터를 가장 잘 표현하는 주성분 벡터(PC)를 기준으로 데이터를 정사영시켜 차원을 축소하는 것이다. 데이터의 분포에서, 분산이 큰 부분은 데이터의 방향을 보여준다. 따라서 분산이 큰 부분을 주성분 벡터로 하여, 데이터의 특성을 유지하면서 차원을 줄여주는것이다. 이 과정을 거치게 되면 행렬 형태의 데이터는 선형변환을 거쳐 축소된 차원의 새로운 행렬로 거듭난다. 쉽게말해 45 차원에서 3차원으로 축소를 한다면, 데이터 하나당 45개씩의 특성이 있는데, 데이터 포인트간의 분포와 분산, 데이터 특성을 최대한 살리면서 45열짜리 행렬을 3열짜리 행렬로 변환시키는 과정이다. 자세한 수식과 선형대수학적인 원리는 다음 링크를 참초하자. 

나는 이번에 PCA를 두 가지 방식으로 활용하고자 한다. 첫 번째로, 데이터를 3차원 평면에 plotting하여 데이터가 어떻게 분포되었는지 보여주기 위해, 데이터를 3차원으로 축소해 그래프를 그릴 것이다. 그러나 이것은 '3차원으로 축소된 데이터' 이기 때문에 실제로 classification을 진행할때 사용되는 데이터와는 차이가 있다. 45개의 특성을 가진 원본 데이터의 특성을 최대한 살려 3차원에 표현한 것이지, 원본 데이터를 보여주는 것이 아니라는 것이다. 

두 번째로, 45개의 feature를 가진 원본 데이터를 이용해 classification을 한번 해보고, PCA를 이용해 데이터를 차원 축소하여 classification을 또 한번 해본 뒤 결과를 비교할 것이다. 

Classification

먼저 위에서 준비한 데이터를 3차원 공간으로 축소해서 데이터의 분포를 그려보자. 

###Plot_pca
#3D plotting wihi Entire Data and label
#original
pca = RandomizedPCA(n_components=3)
reduced_data_pca = pca.fit_transform(np.array(original_data))
colors = ['blue', 'green', 'red']
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(len(colors)):
    x = reduced_data_pca[:, 0][true_label==positions[i]]
    y = reduced_data_pca[:, 1][true_label==positions[i]]
    z = reduced_data_pca[:, 2][true_label==positions[i]]
    ax.scatter(x,y,z, c=colors[i])
plt.legend(positions)
plt.title("3D PCA Scatter Plot - Original Data")
xaxis = ((min(x), max(x)), (0, 0) ,(0, 0))
ax.plot(xaxis[0], xaxis[1], xaxis[2], "yellow")
yaxis = ((0, 0), (min(y), max(y)),(0, 0))
ax.plot(yaxis[0], yaxis[1], yaxis[2], "yellow")
zaxis = ((0, 0) ,(0, 0),(min(z), max(z)))
ax.plot(zaxis[0], zaxis[1], zaxis[2], "yellow")
plt.show()

다시 말하지만 위의 그래프는 PCA를 통해 원본 데이터를 3차원으로 축소해 그린 그래프이다. 즉, 원본 데이터의 특성을 최대한 유지하며 3차원 공간에 표현했지만, 원본 데이터와 실제로 값에 차이가 있다. 

이제 classification을 바로 진행해보자. 일단 차원 축소 없이 진행해보도록 하겠다. 

#Classification

X_train = np.array(original_data)[:10000]
y_train = np.array(original_label)[:10000][:, 0]

X_test =  np.array(original_data)[10000:]
y_test = np.array(original_label)[10000:][:, 0]

knn = neighbors.KNeighborsClassifier()
knn.fit(X_train, y_train)
prediction = knn.predict(X_test)
entire_prediction =  knn.predict(np.array(original_data))
classify_label = prediction

Training 데이터와 Test 데이터로 나누어, Training 데이터를 가지고 모델을 학습시켰다. 즉, 약 14,000명정도 되는 선수 데이터 중 앞의 10000개를 이용해 모델을 학습시키고, 나머지 4000명 가량의 포지션을 예측하고, 실제 포지션과 비교해 정확도를 측정하려고 한다. 이제 classify_label이라는 변수에 knn알고리즘으로 예측한 test data의 레이블 (포지션)이 저장되었다. classify_label 과 정답(원래 포지션)을 비교해 정확도를 측정해보자. 

def accuracy(true, label):
    n = 0
    for i in range(len(label)):
        if true[i]==label[i]:
            n+=1
    return (n/len(label))*100
accuracy_test = accuracy(y_test, classify_label)
print (accuracy_test)

#출력된 결과: 72.64994547437296

약 72프로의 정확도가 나타났다. 즉, KNN을 가지고 측정한 포지션중 72프로가 정확히 맞춰냈다는 것이다. 한번 classification의 결과도 3차원으로 차원 축소를 거쳐 그래프를 그려보겠다. 

#Test Data
pca = RandomizedPCA(n_components=3)
reduced_data_pca = pca.fit_transform(np.array(X_test))
colors = ['blue', 'green', 'red']
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(len(colors)):
    x = reduced_data_pca[:, 0][y_test==positions[i]]
    y = reduced_data_pca[:, 1][y_test==positions[i]]
    z = reduced_data_pca[:, 2][y_test==positions[i]]
    ax.scatter(x,y,z, c=colors[i])
plt.legend(positions)
plt.title("3D PCA Scatter Plot - Test Data True")
xaxis = ((min(x), max(x)), (0, 0) ,(0, 0))
ax.plot(xaxis[0], xaxis[1], xaxis[2], "yellow")
yaxis = ((0, 0), (min(y), max(y)),(0, 0))
ax.plot(yaxis[0], yaxis[1], yaxis[2], "yellow")
zaxis = ((0, 0) ,(0, 0),(min(z), max(z)))
ax.plot(zaxis[0], zaxis[1], zaxis[2], "yellow")
plt.show()

#Classified
pca = RandomizedPCA(n_components=3)
reduced_data_pca = pca.fit_transform(np.array(X_test))
colors = ['blue', 'green', 'red']
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
for i in range(len(colors)):
    x = reduced_data_pca[:, 0][classify_label==positions[i]]
    y = reduced_data_pca[:, 1][classify_label==positions[i]]
    z = reduced_data_pca[:, 2][classify_label==positions[i]]
    ax.scatter(x,y,z, c=colors[i])
plt.legend(positions)
plt.title("3D PCA Scatter Plot - Test Data Labeled")
xaxis = ((min(x), max(x)), (0, 0) ,(0, 0))
ax.plot(xaxis[0], xaxis[1], xaxis[2], "yellow")
yaxis = ((0, 0), (min(y), max(y)),(0, 0))
ax.plot(yaxis[0], yaxis[1], yaxis[2], "yellow")
zaxis = ((0, 0) ,(0, 0),(min(z), max(z)))
ax.plot(zaxis[0], zaxis[1], zaxis[2], "yellow")
plt.show()

위에가 Test 데이터의 실제 레이블, 아래가 Classify된 레이블이다. 전체적으로 센터는 꽤 정확히 예측한 모양이지만, 가드와 포워드가 많이 뒤섞인 모습을 보여준다. 아마 72프로에서 예측이 빗나간 30프로정도는 대부분 포워드와 가드 포지션때문이지 않을까 싶다. 뒤의 분석에서 더 이야기하겠지만 특히 현대 농구에서 포워드가 스몰 포워드, 파워 포워드 등으로 세분화되면서  특히 스몰 포워드의 경우에는 가드와 역할의 경계가 무뎌지는 모습을 보여주고 있다. 이러한 포지션 장벽의 허물어짐이 두 포지션의 구별을 어렵게 한 것이 아닐까 싶다. 

그렇다면 세 포지션중 어떤 포지션에 대한 예측이 가장 정확했을까? 포지션별 정확도와, 포지션별 예측 결과를 추출해보자.

Centers = df.loc[df["New_Pos"] == "Center"]._get_numeric_data()
Guards = df.loc[df["New_Pos"] == "Guard"]._get_numeric_data()
Forwards = df.loc[df["New_Pos"] == "Forward"]._get_numeric_data()
    
del Centers["Unnamed: 0"]
del Centers["Year"]
del Centers["Age"]

del Forwards["Unnamed: 0"]
del Forwards["Year"]
del Forwards["Age"]

del Guards["Unnamed: 0"]
del Guards["Year"]
del Guards["Age"]

Centers = np.array(Centers)
Forwards = np.array(Forwards)
Guards = np.array(Guards)

C_prediction = knn.predict(Centers)
F_prediction = knn.predict(Forwards)
G_prediction= knn.predict(Guards)

from collections import Counter

print (Counter(C_prediction),Counter(F_prediction),Counter(G_prediction) )
C_Accuracy = (Counter(C_prediction)["Center"]/len(C_prediction))*100
F_Accuracy = (Counter(F_prediction)["Forward"]/len(F_prediction))*100
G_Accuracy = (Counter(G_prediction)["Guard"]/len(G_prediction))*100

C_count  = dict(Counter(C_prediction))
G_count  = dict(Counter(G_prediction))
F_count  = dict(Counter(F_prediction))

#출력된 결과:
C_prediction: 53.53798126951092

F_prediction: 78.0223501523874

G_prediction: 89.18158946277934

가드 포지션의 경우 거의 90프로의 확률로 정확히 예측했고, 포워드는 78프로, 센터는 의외로 50프로정도밖에 맞추지 못했다. 왜 이런결과가 나왔을까? 포지션별 예측 결과를 보면 다음과 같다:

C_count
{'Center': 1029, 'Forward': 878, 'Guard': 15}

G_count
{'Center': 25, 'Forward': 706, 'Guard': 6026}

F_count
{'Center': 404, 'Forward': 4608, 'Guard': 894}

Analysis - 분석

여기서 흥미로운 사실을 알 수 있다. 센터 포지션인 선수를 가드라고 판단한 경우는 약 2000개의 데이터중 15경우뿐으로 1프로가 되지 않는다. 그러나 센터의 경우 '포워드'라고 예측한 비율이 상당히 높아 전체적인 정확도가 낮게 나타났다. 반대로, 가드 포지션인 선수를 센터라고 판단한 경우도 약 7000개의 데이터 중 25개 뿐으로,  0.3프로정도밖에 되지 않는다. 그러나 가드를 포워드라고 판단한 경우는 약 10프로정도가 있다. 그럼 포워드는 어떤가? 약 80프로를 올바르게 예측했지만, 포워드를 가드라고 예측한 경우, 그리고 센터라고 예측한 비율이 작지는 않다. 

이러한 결과는 포지션의 특성과 밀접한 관련이 있는 것으로 보인다. 이 데이터에 따르면 센터와 가드는 상대적으로 특성이 겹치지 않고, 멀리 떨어져있는 포지션이다. 반면 포워드는 센터와 가드 두 포지션 모두와 어느정도 특성을 공유하는 포지션이라는 말이 된다. 

사실이다. 가드는 외곽에서 공격을 하고, 슛, 드리블, 공격의 운영을 주로 한다면 센터는 골 밑을 지키며 적극적으로 몸싸움을 하고 리바운드, 수비, 블락을 하는 비율이 더 높다. 그렇기에 센터와 가드의 특성은 분명히 갈린다. 대부분의 가드는 센터에 비해 슛을 잘 쏘고 드리블에 강점을 보이겠지만 신장이 작고 몸싸움이나 리바운드에 약점을 보인다. 반면 포워드는 보통 위치상으로 외곽과 골대 중앙의 사이 어딘가에 위치하는데 가드의 성향을 어느정도 가진 선수들도 있으며, 센터의 성향을 가진 선수들도 많다. 

이 데이터셋 전체에서 센터 성향의 포워드가 많았음은 분명하다. 그렇기에 센터인 선수들 중 약 40프로를 포워드로 판단했을 것이다. 그러나 반대로 포워드인 선수들 중 센터일 것이라고 판단한 경우는 그렇게 많지 않았다. 아마 학습 데이터의 양 차이가 만들어낸 결과일 것이다.  전체 데이터중 센터는 1922명, 포워드는 5906명, 가드는 6757명 이었다. 상대적으로 센터에대한 데이터가 평균 3배가량 차이가 나도록 적다보니, classificaition 모델 자체가 '센터'포지션에 대해 충분히 학습하지 못한것이다. 그래서 센터의 성향을 띈 포워드와 센터를 구분하는데 어려움을 가졌다. 반편 포워드에 대해서는 충분한 데이터로 학습을 거쳤기 때문에 센터와 '센터같은 포워드'를 비교적 잘 구별해내었다. 

부록 - PCA 적용해서 classify해보기 

위의 과정에서 우리는 3차원 공간안에 데이터를 그리기 위해서만 PCA를 사용하였다. 부록으로, 45개의 특성 전체를 PCA 차원축소를 거친 후 classification을 수행해보고 얼마나 결과가 차이나는지를 살펴보겠다. 

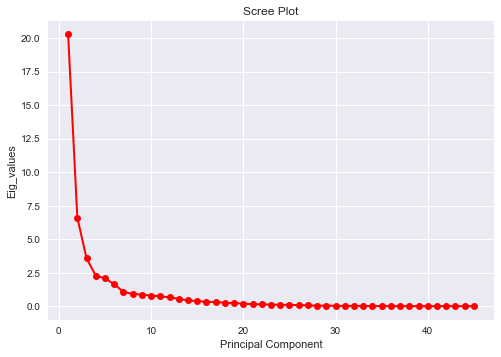
먼저 45차원인 이 데이터를 몇 차원으로 축소할 것인지를 정해야 한다. 이 자료와 구글링을 통해 알아분 후 Scree plot을 그리는 방법을 택했다. 차원에 따른 데이터 행렬의 eigenvalue (고유값)이 급격하게 커지는 구간을 차원의 수로 정하는 방법이다. (자세한 내용은 위의 자료를 참고하자)

#Finding fight number of PCs
from sklearn.preprocessing import StandardScaler
X_std_train = StandardScaler().fit_transform(original_data)
mean_vec_train = np.mean(X_std_train, axis = 0)
cov_mat_train = (X_std_train - mean_vec_train).T.dot((X_std_train - mean_vec_train))/(X_std_train.shape[0]-1)

cov_mat_train = np.cov(X_std_train.T)
eig_vals_train, eig_vecs_train = np.linalg.eig(cov_mat_train)

sing_vals = np.arange(len(eig_vals_train))+1
plt.plot(sing_vals, eig_vals_train, "ro-", linewidth=2)
plt.title("Scree Plot")
plt.xlabel("Principal Component")
plt.ylabel("Eig_values")
plt.show()

Principal Component (차원의수 = label의 수) 가 4개인 지점을 기점으로 kink (꺾인 부분)가 발생함을 볼 수 있다. 따라서 차원의 수를 4개까지 축소하는것으로 정한다. 

---

pca = RandomizedPCA(n_components=4)
original_data = pca.fit_transform(np.array(original_data))
#Classification

X_train = np.array(original_data)[:10000]
y_train = np.array(original_label)[:10000][:, 0]

X_test =  np.array(original_data)[10000:]
y_test = np.array(original_label)[10000:][:, 0]

knn = neighbors.KNeighborsClassifier()
knn.fit(X_train, y_train)
prediction = knn.predict(X_test)
classify_label = prediction

def accuracy(true, label):
    n = 0
    for i in range(len(label)):
        if true[i]==label[i]:
            n+=1
    return (n/len(label))*100

accuracy_test = accuracy(y_test, classify_label)

print ("Accuracy is: ", accuracy_test)
#출력된 값:
Accuracy is:  72.49727371864776

아까와 같이 정확도를 계산해보면 약 72프로로 PCA를 적용하지 않았을 때와 거의 같은 정확도가 나온다. 이는 두 가지중 한가지를 의미한다고 생각한다. 첫째, 45개의 특성이 모두 '포지션'이라는 class를 설명하기 적절한 특성들이어서 차원을 축소하지 않아도 정확한 결과를 얻을 수 있거나, 둘째, 위에서 말한것처럼 포지션의 경계가 분명하지 않아서 72프로보다 높은 정확도를 보이기 힘든 것이지 않을까 싶다. 

---

참고 링크:

https://towardsdatascience.com/dimensionality-reduction-does-pca-really-improve-classification-outcome-6e9ba21f0a32

http://thesciencelife.com/archives/1001

https://plot.ly/ipython-notebooks/principal-component-analysis/

https://wikidocs.net/7646